darkliner.blogg.se - Calculus equations

The displacement and motion problems also find their applications of integrals. Definite integrals form the powerful tool to find the area under simple curves, the area bounded by a curve and a line, the area between two curves, the volume of the solids. Using integration, we can find the distance given the velocity. To find ∫ f(x)/g(x) dx, decompose this improper rational function to a proper rational function and then integrate. Integration of rational algebraic functions whose numerator and denominator contain positive integral powers of x with constant coefficients is done by resolving them into partial fractions. Finding Integrals by Integration by Partial Fractions If two functions are of the product form, integrals are found by the method of integration by parts. Finding Integrals by Integration by Parts If u is a function of x, then u' = du/dx. Finding integrals by integration by partial fractions.Ī few integrals are found by the substitution method.Finding integrals by integration by parts.Finding integrals by integration by substitution method.There are several methods adopted for finding the indefinite integrals. The prominent methods are: We specify an integral of a function over an interval on which the integral is defined. The area of a region is found by breaking it into thin vertical rectangles and applying the lower and the upper limits, the area of the region is summed up. A definite integral of a function can be represented as the area of the region bounded by its graph of the given function between two points in the line. We approximate the actual value of an integral by drawing rectangles. Integral is the representation of the area of a region under a curve. If g(x) = 2x, then anti-derivative of g(x) = ∫ g(x) = x 2 Definition of Integralį(x) is called an antiderivative or Newton-Leibnitz integral or primitive of a function f(x) on an interval I. Here, the function f is called antiderivative or integral of f’. Given the derivative f’ of the function f, we can determine the function f. Integrals assign numbers to functions in a way that describe displacement and motion problems, area and volume problems, and so on that arise by combining all the small data. The process of getting f(x) from f'(x) is called integration. Add a multiple of one row to a different row.Integrals are the values of the function found by the process of integration.To solve a system of linear equations, reduce the corresponding augmented matrix to row-echelon form using the Elementary Row Operations: Solving systems of linear equations by reducing the augmented matrices In the Exploration, use the Row Reduction Calculator to practice

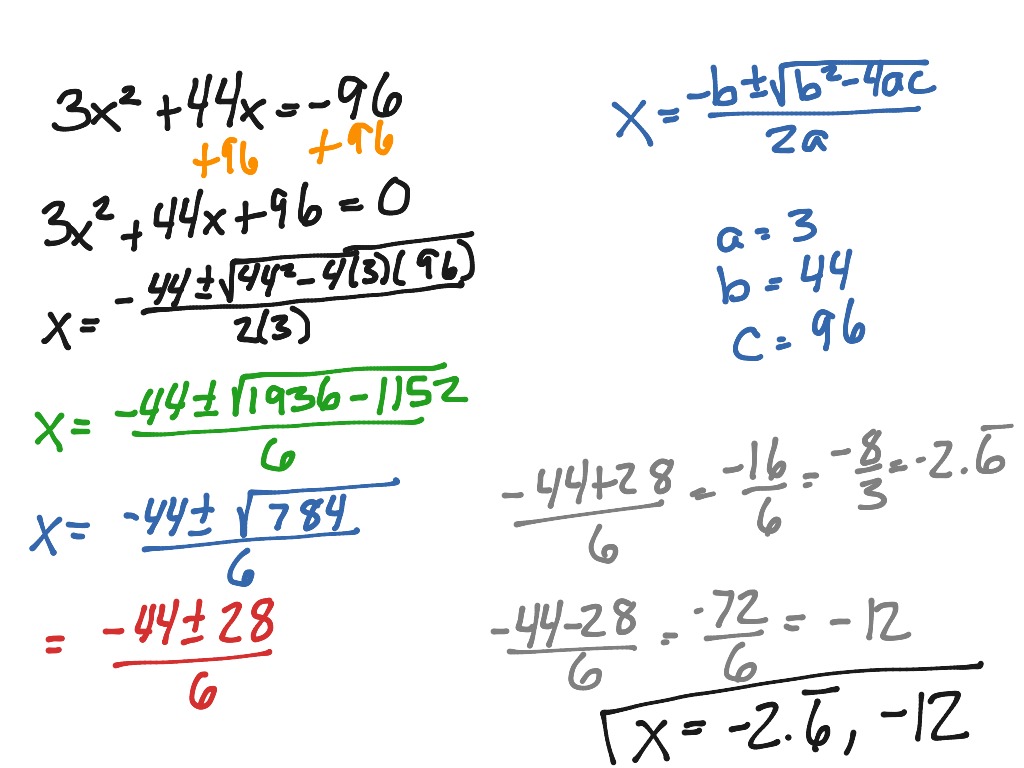
Thus, the solution of the original system is $x_1=2, \quad x_2=-1, We have brought the matrix to row-echelon form. The Gaussian Elimination algorithm proceeds as follows:

We will use Gaussian Elimination to solve the linear system

A more computationally-intensive algorithm that takes a matrix to reduced row-echelon form is given by the Gauss-Jordon Reduction.

For instance, in Step 2 you often have a choice of rows to move to the top.

In practice, you have some flexibility in the application of the algorithm.

Repeat steps 1$-$4 on the rows still being worked on.

Subtract multiples of that row from the rows below it to makeĮach entry below the leading 1 zero.

Multiply that row by $1/a$ to create a leading 1.

Otherwise, find the first column from the left with a non-zeroĮntry $a$ and move the row containing that entry to the top of the.

If the matrix is already in row-echelon form, then stop.Solving Systems of Linear Equations Row Reduction – HMC Calculus Tutorial